TensorFlow ML cookbook 第三章6-8节 套索和岭回归、弹性网络回归and Logistic回归

问题导读：
1、如何实现套索和岭回归？
2、如何实现弹性网络回归？
3、如何实施Logistic回归？
4、如何理解将线性回归转化为二元分类？





上一篇:TensorFlow ML cookbook 第三章4、5节 理解线性回归中的损失函数和实施戴明回归

实现套索和岭回归

这里也有办法限制系数对回归输出的影响。 这些方法被称为正则化方法，两种最常见的正则化方法是套索和岭回归。 我们介绍如何在这个章节中实现这两个。

准备好
除了我们加入正则化项以限制公式中的斜率（或偏斜率）之外，Lasso和岭回归与常规线性回归非常相似。这可能有多种原因，但常见的原因是我们希望限制对因变量有影响的功能。这可以通过向损失函数添加一个项来完成，该项取决于我们的斜率值A。

对于套索回归，如果斜率A超过某个值，我们必须添加一个可以大大增加损失函数的项。我们可以使用TensorFlow的逻辑运算，但它们没有与它们相关的梯度。相反，我们将使用一个连续的近似步进函数，称为连续重步函数，这个函数被放大并转换到我们选择的正则化截止点。我们将很快展示如何进行套索回归。

对于岭回归，我们只是给L2范数添加一个项，这是斜率系数的缩放L2范数。这个修改很简单，在这个章节的最后有更多...部分。

怎么做
1.我们将再次使用虹膜数据集并以与之前相同的方式设置我们的脚本。 我们首先加载库，启动会话，加载数据，声明批量大小，创建占位符，变量和模型输出，如下所示：

[mw_shl_code=python,true]import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
ops.reset_default_graph()
sess = tf.Session()
iris = datasets.load_iris()
x_vals = np.array([x[3] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data])
batch_size = 50
learning_rate = 0.001
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
A = tf.Variable(tf.random_normal(shape=[1,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
model_output = tf.add(tf.matmul(x_data, A), b)[/mw_shl_code]


2.我们增加了损失函数，这是一个修改后的连续重度阶梯函数。 我们还将套索回归的截止值设置为0.9。 这意味着我们要限制斜率系数小于0.9。 使用下面的代码：
[mw_shl_code=python,true]lasso_param = tf.constant(0.9)
heavyside_step = tf.truediv(1., tf.add(1., tf.exp(tf.mul(-100., tf.sub(A, lasso_param)))))
regularization_param = tf.mul(heavyside_step, 99.)
loss = tf.add(tf.reduce_mean(tf.square(y_target - model_output)), regularization_param)[/mw_shl_code]

3.我们现在初始化我们的变量并声明我们的优化器，如下所示：
[mw_shl_code=python,true]init = tf.global_variables_initializer()
sess.run(init)
my_opt = tf.train.GradientDescentOptimizer(learning_rate)
train_step = my_opt.minimize(loss) [/mw_shl_code]

4.我们将再次运行训练循环，因为它可能需要一段时间才能收敛。 我们可以看到斜率系数小于0.9。 使用下面的代码：
[mw_shl_code=python,true]loss_vec = []
for i in range(1500):
  rand_index = np.random.choice(len(x_vals), size=batch_size)
  rand_x = np.transpose([x_vals[rand_index]])
  rand_y = np.transpose([y_vals[rand_index]])
  sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
  temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_ target: rand_y})
  loss_vec.append(temp_loss[0])
  if (i+1)%300==0:
    print('Step #''' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
    print('Loss = ' + str(temp_loss))
Step #300 A = [[ 0.82512331]] b = [[ 2.30319238]]
Loss = [[ 6.84168959]]

Step #600 A = [[ 0.8200165]] b = [[ 3.45292258]]
Loss = [[ 2.02759886]]
Step #900 A = [[ 0.81428504]] b = [[ 4.08901262]]
Loss = [[ 0.49081498]]
Step #1200 A = [[ 0.80919558]] b = [[ 4.43668795]]
Loss = [[ 0.40478843]]
Step #1500 A = [[ 0.80433637]] b = [[ 4.6360755]]
Loss = [[ 0.23839757]] [/mw_shl_code]

怎么运行
我们通过向线性回归的损失函数添加连续的超重阶跃函数来实现套索回归。 由于阶梯函数的陡峭性，我们必须小心步长。 太大的步长，它不会收敛。 对于岭回归，请参阅下一节中的必要更改。

还有更多
对于岭回归，我们将损失函数更改为如下代码所示：
[mw_shl_code=python,true]ridge_param = tf.constant(1.)
ridge_loss = tf.reduce_mean(tf.square(A))
loss = tf.expand_dims(tf.add(tf.reduce_mean(tf.square(y_target - model_output)), tf.mul(ridge_param, ridge_loss)), 0) [/mw_shl_code]

实现弹性网络回归
弹性净回归是一种回归方法，它通过在损失函数中加入L1和L2正则化项来将套索回归和岭回归相结合。

准备好
在前两个配方之后实现弹性网络回归应该很简单，因此我们将在虹膜数据集上进行多重线性回归，而不是像以前那样坚持二维数据。 我们将使用踏板长度，踏板宽度和萼片宽度来预测萼片长度。

怎么做
1.首先我们加载必要的库并初始化一个图，如下所示：
[mw_shl_code=python,true]import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
sess = tf.Session() [/mw_shl_code]

2.现在我们将加载数据。 这一次，x数据的每个元素将是一个三个值的列表，而不是一个。 使用下面的代码：
[mw_shl_code=python,true]iris = datasets.load_iris()
x_vals = np.array([[x[1], x[2], x[3]] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data]) [/mw_shl_code]

3.接下来我们声明批量大小，占位符，变量和模型输出。 这里唯一的区别是，我们更改了x数据占位符的大小规格以取三个值而不是一个，如下所示：
[mw_shl_code=python,true]batch_size = 50
learning_rate = 0.001
x_data = tf.placeholder(shape=[None, 3], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
A = tf.Variable(tf.random_normal(shape=[3,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
model_output = tf.add(tf.matmul(x_data, A), b) [/mw_shl_code]

4.对弹性网而言，损失函数具有部分斜率的L1和L2范数。 我们创建这些条款，然后将它们添加到损失函数中，如下所示：
[mw_shl_code=python,true]elastic_param1 = tf.constant(1.)
elastic_param2 = tf.constant(1.)
l1_a_loss = tf.reduce_mean(tf.abs(A))
l2_a_loss = tf.reduce_mean(tf.square(A))
e1_term = tf.mul(elastic_param1, l1_a_loss)
e2_term = tf.mul(elastic_param2, l2_a_loss)
loss = tf.expand_dims(tf.add(tf.add(tf.reduce_mean(tf.square(y_ target - model_output)), e1_term), e2_term), 0) [/mw_shl_code]

5.现在我们可以初始化变量，声明我们的优化器，然后运行训练循环并拟合我们的系数，如下所示：
[mw_shl_code=python,true]init = tf.global_variables_initializer()
sess.run(init)
my_opt = tf.train.GradientDescentOptimizer(learning_rate)
train_step = my_opt.minimize(loss)
loss_vec = []

for i in range(1000):
  rand_index = np.random.choice(len(x_vals), size=batch_size)
  rand_x = x_vals[rand_index]
  rand_y = np.transpose([y_vals[rand_index]])
  sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
  temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_ target: rand_y})
  loss_vec.append(temp_loss[0])
  if (i+1)%250==0:
    print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
    print('Loss = ' + str(temp_loss)) [/mw_shl_code]

6.这里是代码的输出：

[mw_shl_code=python,true]Step #250 A = [[ 0.42095602]
[ 0.1055888 ]
[ 1.77064979]] b = [[ 1.76164341]]
Loss = [ 2.87764359]
Step #500 A = [[ 0.62762028]
[ 0.06065864]
[ 1.36294949]] b = [[ 1.87629771]]
Loss = [ 1.8032167]
Step #750 A = [[ 0.67953539]
[ 0.102514 ]
[ 1.06914485]] b = [[ 1.95604002]]
Loss = [ 1.33256555]
Step #1000 A = [[ 0.6777274 ]
[ 0.16535147]
[ 0.8403284 ]] b = [[ 2.02246833]]
Loss = [ 1.21458709] [/mw_shl_code]

7.现在我们可以观察到训练迭代的损失，以确保它收敛，如下所示：
[mw_shl_code=python,true]plt.plot(loss_vec, 'k-')
plt.title('Loss' per Generation')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()[/mw_shl_code]

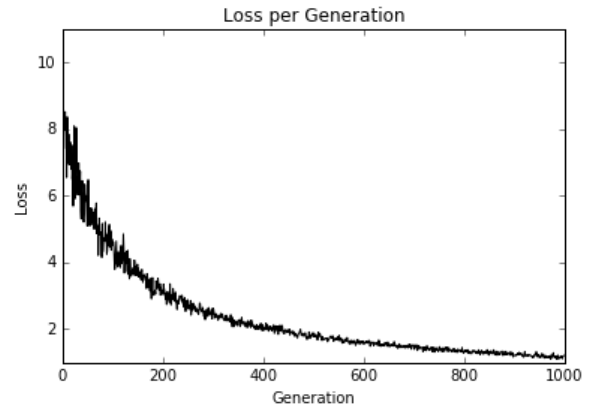
图10：1000次训练迭代绘制的弹性净回归损失

怎么运行
这里实施弹性净回归以及多元线性回归。我们可以看到，在损失函数中使用这些正则化项时，收敛速度比以前的部分慢。正则化就像在损失函数中添加适当的术语一样简单。

实施Logistic回归
对于这个配方，我们将实施逻辑回归来预测低出生体重的概率。

准备好
逻辑回归是将线性回归转化为二元分类的一种方法。这是通过在一个sigmoid函数中转换线性输出来实现的，该函数将输出在0和1之间进行缩放。目标是0或1，表示数据点是否在一个类中或另一个类中。由于我们预测的是0或1之间的数字，如果预测高于指定的截止值，则预测被分类到类别值1'''中，否则将类别0分类。为了这个例子的目的，我们将指定中断为0.5，这将使分类变得简单，就像对输出进行四舍五入。

我们将用于这个例子的数据将是通过马萨诸塞大学阿默斯特统计数据库存储库（https://www.umass.edu/statdata/statdata/）获得的低出生体重数据。我们将从其他几个因素预测低出生体重。

怎么做
1.我们首先加载库，包括请求库，因为我们将通过超链接访问低出生体重数据。我们也将开始会议：
[mw_shl_code=python,true]import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import requests
from sklearn import datasets
from sklearn.preprocessing import normalize
from tensorflow.python.framework import ops
ops.reset_default_graph()
sess = tf.Session() [/mw_shl_code]
请注意，在我们缩放数据集之前，我们将数据集分解为训练和测试。 这是一个重要的区别。 我们希望确保训练集完全不影响测试集。 如果我们在分割之前缩放整个集合，那么我们不能保证它们不会相互影响。

2.接下来，我们将通过请求模块加载数据并指定我们要使用的功能。 我们必须具体，因为一个特征是实际的出生体重，我们不希望用这个来预测出生体重是大于还是小于特定量。 我们也不希望将ID列用作预测因子：
[mw_shl_code=python,true]birthdata_url = 'https://www.umass.edu/statdata/statdata/data/ lowbwt.dat'
birth_file = requests.get(birthdata_url)
birth_data = birth_file.text.split('\r\n')[5:]
birth_header = [x for x in birth_data[0].split( '') if len(x)>=1]
birth_data = [[float(x) for x in y.split( '') if len(x)>=1] for y in birth_data[1:] if len(y)>=1]
y_vals = np.array([x[1] for x in birth_data])
x_vals = np.array([x[2:9] for x in birth_data]) [/mw_shl_code]

3.首先我们将数据集分解为测试和训练集：
[mw_shl_code=python,true]train_indices = np.random.choice(len(x_vals), round(len(x_ vals)*0.8), replace=False)
test_indices = np.array(list(set(range(len(x_vals))) - set(train_ indices)))
x_vals_train = x_vals[train_indices]
x_vals_test = x_vals[test_indices]
y_vals_train = y_vals[train_indices]
y_vals_test = y_vals[test_indices]
[/mw_shl_code]


4.当特征在0和1之间缩放（最小 - 最大比例缩放）时，Logistic回归收敛效果更好。 接下来我们将扩展每个功能：
[mw_shl_code=python,true]def normalize_cols(m):
  col_max = m.max(axis=0)
  col_min = m.min(axis=0)
  return (m-col_min) / (col_max - col_min)
x_vals_train = np.nan_to_num(normalize_cols(x_vals_train))
x_vals_test = np.nan_to_num(normalize_cols(x_vals_test)) [/mw_shl_code]
请注意，在我们缩放数据集之前，我们将数据集分解为训练和测试。 这是一个重要的区别。 我们希望确保训练集完全不影响测试集。 如果我们在分割之前缩放整个集合，那么我们不能保证它们不会相互影响。

5.现在我们可以开始我们的训练循环并记录损失和准确度：
[mw_shl_code=python,true]loss_vec = []
train_acc = []
test_acc = []
for i in range(1500):
  rand_index = np.random.choice(len(x_vals_train), size=batch_ size)
  rand_x = x_vals_train[rand_index]
  rand_y = np.transpose([y_vals_train[rand_index]])
  sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
  temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_ target: rand_y})
  loss_vec.append(temp_loss)
  temp_acc_train = sess.run(accuracy, feed_dict={x_data: x_vals_ train, y_target: np.transpose([y_vals_train])})
  train_acc.append(temp_acc_train)
  temp_acc_test = sess.run(accuracy, feed_dict={x_data: x_vals_ test, y_target: np.transpose([y_vals_test])})
  test_acc.append(temp_acc_test) [/mw_shl_code]

6.这里是代码来看看损失和准确性的情节：
[mw_shl_code=python,true]plt.plot(loss_vec, 'k-')
plt.title('Cross Entropy Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('Cross' Entropy Loss')
plt.show()
plt.plot(train_acc, 'k-', label='Train Set Accuracy')
plt.plot(test_acc, 'r--', label='Test Set Accuracy')
plt.title('Train' and Test Accuracy')
plt.xlabel('Generation')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()[/mw_shl_code]

怎么运行
这是迭代和训练和测试集精度的损失。 由于数据集只有189个观测值，因此数据集的随机分裂会导致列车和测试精度图变化：

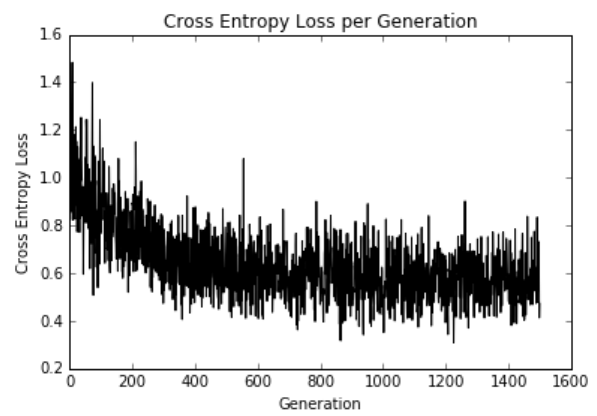
图11：在1,500次迭代过程中绘制的交叉熵损失

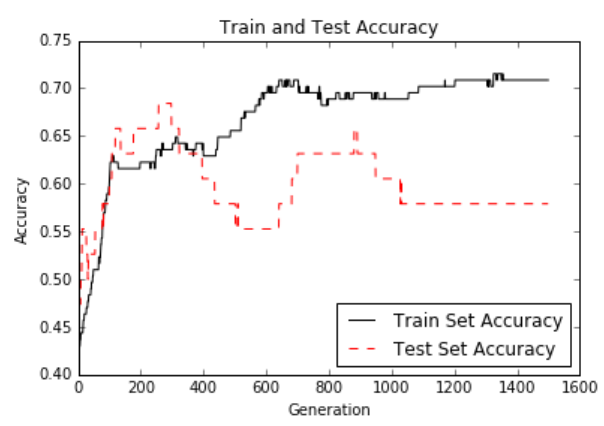
图12：超过1,500代的测试和训练集精度。


原文：
Implementing Lasso and Ridge Regression
There are also ways to limit the influence of coefficients on the regression output. These methods are called regularization methods and two of the most common regularization methods are lasso and ridge regression. We cover how to implement both of these in this recipe.


Getting ready
Lasso and ridge regression are very similar to regular linear regression, except we adding regularization terms to limit the slopes (or partial slopes) in the formula. There may be multiple reasons for this, but a common one is that we wish to restrict the features that have an impact on the dependent variable. This can be accomplished by adding a term to the loss function that depends on the value of our slope, A.


For lasso regression, we must add a term that greatly increases our loss function if the slope, A, gets above a certain value. We could use TensorFlow's logical operations, but they do not have a gradient associated with them. Instead, we will use a continuous approximation to a step function, called the continuous heavy step function, that is scaled up and over to the regularization cut off we choose. We will show how to do lasso regression shortly.
For ridge regression, we just add a term to the L2 norm, which is the scaled L2 norm of the slope coefficient. This modification is simple and is shown in the There's more… section at the end of this recipe.


How to do it…
1.We will use the iris dataset again and set up our script the same way as before. We first load the libraries, start a session, load the data, declare the batch size, create the placeholders, variables, and model output as follows:

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
from tensorflow.python.framework import ops
ops.reset_default_graph()
sess = tf.Session()
iris = datasets.load_iris()
x_vals = np.array([x[3] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data])
batch_size = 50
learning_rate = 0.001
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
A = tf.Variable(tf.random_normal(shape=[1,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
model_output = tf.add(tf.matmul(x_data, A), b)

2.We add the loss function, which is a modified continuous heavyside step function. We also set the cutoff for lasso regression at 0.9. This means that we want to restrict the slope coefficient to be less than 0.9. Use the following code:

lasso_param = tf.constant(0.9)
heavyside_step = tf.truediv(1., tf.add(1., tf.exp(tf.mul(-100., tf.sub(A, lasso_param)))))
regularization_param = tf.mul(heavyside_step, 99.)
loss = tf.add(tf.reduce_mean(tf.square(y_target - model_output)), regularization_param)


3.We now initialize our variables and declare our optimizer, as follows:

init = tf.global_variables_initializer()
sess.run(init)
my_opt = tf.train.GradientDescentOptimizer(learning_rate)
train_step = my_opt.minimize(loss)


4.We will run the training loop a fair bit longer because it can take a while to converge. We can see that the slope coefficient is less than 0.9. Use the following code:

loss_vec = []
for i in range(1500):
rand_index = np.random.choice(len(x_vals), size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_ target: rand_y})
loss_vec.append(temp_loss[0])
if (i+1)%300==0:
print('Step #''' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
print('Loss = ' + str(temp_loss))
Step #300 A = [[ 0.82512331]] b = [[ 2.30319238]]
Loss = [[ 6.84168959]]

Step #600 A = [[ 0.8200165]] b = [[ 3.45292258]]
Loss = [[ 2.02759886]]
Step #900 A = [[ 0.81428504]] b = [[ 4.08901262]]
Loss = [[ 0.49081498]]
Step #1200 A = [[ 0.80919558]] b = [[ 4.43668795]]
Loss = [[ 0.40478843]]
Step #1500 A = [[ 0.80433637]] b = [[ 4.6360755]]
Loss = [[ 0.23839757]]


How it works…
We implement lasso regression by adding a continuous heavyside step function to the loss function of linear regression. Because of the steepness of the step function, we have to be careful with the step size. Too big of a step size and it will not converge. For ridge regression, see the necessary change in the next section.


There's' more…
For ridge regression, we change the loss function to look like the following code:
ridge_param = tf.constant(1.)
ridge_loss = tf.reduce_mean(tf.square(A))
loss = tf.expand_dims(tf.add(tf.reduce_mean(tf.square(y_target - model_output)), tf.mul(ridge_param, ridge_loss)), 0)


Implementing Elastic Net Regression
Elastic net regression is a type of regression that combines lasso regression with ridge regression by adding a L1 and L2 regularization term to the loss function.


Getting ready
Implementing elastic net regression should be straightforward after the previous two recipes, so we will implement this in multiple linear regression on the iris dataset, instead of sticking to the two-dimensional data as before. We will use pedal length, pedal width, and sepal width to predict sepal length.

How to do it…
1.First we load the necessary libraries and initialize a graph, as follows:

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
sess = tf.Session()


2.Now we will load the data. This time, each element of x data will be a list of three values instead of one. Use the following code:

iris = datasets.load_iris()
x_vals = np.array([[x[1], x[2], x[3]] for x in iris.data])
y_vals = np.array([y[0] for y in iris.data])


3.Next we declare the batch size, placeholders, variables, and model output. The only difference here is that we change the size specifications of the x data placeholder to take three values instead of one, as follows:

batch_size = 50
learning_rate = 0.001
x_data = tf.placeholder(shape=[None, 3], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
A = tf.Variable(tf.random_normal(shape=[3,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
model_output = tf.add(tf.matmul(x_data, A), b)


4.For elastic net, the loss function has the L1 and L2 norms of the partial slopes. We create these terms and then add them into the loss function, as follows:

elastic_param1 = tf.constant(1.)
elastic_param2 = tf.constant(1.)
l1_a_loss = tf.reduce_mean(tf.abs(A))
l2_a_loss = tf.reduce_mean(tf.square(A))
e1_term = tf.mul(elastic_param1, l1_a_loss)
e2_term = tf.mul(elastic_param2, l2_a_loss)
loss = tf.expand_dims(tf.add(tf.add(tf.reduce_mean(tf.square(y_ target - model_output)), e1_term), e2_term), 0)
5.Now we can initialize the variables, declare our optimizer, and run the training loop and fit our coefficients, as follows:

init = tf.global_variables_initializer()
sess.run(init)
my_opt = tf.train.GradientDescentOptimizer(learning_rate)
train_step = my_opt.minimize(loss)
loss_vec = []

for i in range(1000):
  rand_index = np.random.choice(len(x_vals), size=batch_size)
  rand_x = x_vals[rand_index]
  rand_y = np.transpose([y_vals[rand_index]])
  sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
  temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_ target: rand_y})
  loss_vec.append(temp_loss[0])
  if (i+1)%250==0:
    print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
    print('Loss = ' + str(temp_loss))


6.Here is the output of the code:

Step #250 A = [[ 0.42095602]
[ 0.1055888 ]
[ 1.77064979]] b = [[ 1.76164341]]
Loss = [ 2.87764359]
Step #500 A = [[ 0.62762028]
[ 0.06065864]
[ 1.36294949]] b = [[ 1.87629771]]
Loss = [ 1.8032167]
Step #750 A = [[ 0.67953539]
[ 0.102514 ]
[ 1.06914485]] b = [[ 1.95604002]]
Loss = [ 1.33256555]
Step #1000 A = [[ 0.6777274 ]
[ 0.16535147]
[ 0.8403284 ]] b = [[ 2.02246833]]
Loss = [ 1.21458709]


7.Now we can observe the loss over the training iterations to be sure that it converged, as follows:

plt.plot(loss_vec, 'k-')
plt.title('Loss' per Generation')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()

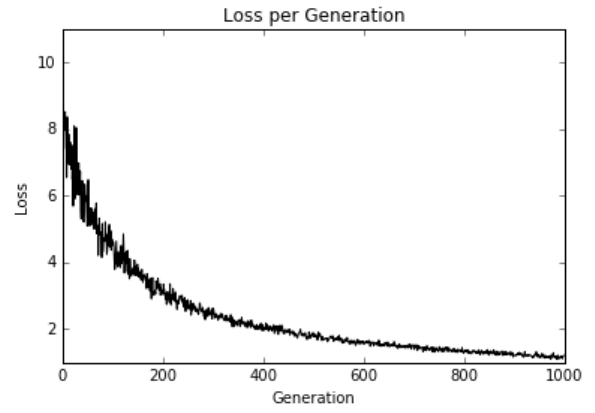
Figure 10: Elastic net regression loss plotted over the 1,000 training iterations


How it works…
Elastic net regression is implemented here as well as multiple linear regression. We can see that with these regularization terms in the loss function the convergence is slower than in prior sections. Regularization is as simple as adding in the appropriate terms in the loss functions.


Implementing Logistic Regression
For this recipe, we will implement logistic regression to predict the probability of low birthweight.


Getting ready
Logistic regression is a way to turn linear regression into a binary classification. This is accomplished by transforming the linear output in a sigmoid function that scales the output between zero and 1. The target is a zero or 1, which indicates whether or not a data point is in one class or another. Since we are predicting a number between zero or 1, the prediction is classified into class value 1''' if the prediction is above a specified cut off value and class 0 otherwise. For the purpose of this example, we will specify that cut off to be 0.5, which will make the classification as simple as rounding the output.

The data we will use for this example will be the low birthweight data that is obtained through the University of Massachusetts Amherst statistical dataset repository (https://www. umass.edu/statdata/statdata/). We will be predicting low birthweight from several other factors.


How to do it…
1.We start by loading the libraries, including the request library, because we will access the low birth weight data through a hyperlink. We will also initiate a session:

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import requests
from sklearn import datasets
from sklearn.preprocessing import normalize
from tensorflow.python.framework import ops
ops.reset_default_graph()
sess = tf.Session()
Note that we split the dataset into train and test before we scaled the dataset. This is an important distinction to make. We want to make sure that the training set does not influence the test set at all. If we scaled the whole set before splitting, then we cannot guarantee that they don't influence each other.

2.Next we will load the data through the request module and specify which features we want to use. We have to be specific because one feature is the actual birth weight and we don't want to use this to predict if the birthweight is greater or less than a specific amount. We also do not want to use the ID column as a predictor either:

birthdata_url = 'https://www.umass.edu/statdata/statdata/data/ lowbwt.dat'
birth_file = requests.get(birthdata_url)
birth_data = birth_file.text.split('\r\n')[5:]
birth_header = [x for x in birth_data[0].split( '') if len(x)>=1]
birth_data = [[float(x) for x in y.split( '') if len(x)>=1] for y in birth_data[1:] if len(y)>=1]
y_vals = np.array([x[1] for x in birth_data])
x_vals = np.array([x[2:9] for x in birth_data])


3.First we split the dataset into test and train sets:

train_indices = np.random.choice(len(x_vals), round(len(x_ vals)*0.8), replace=False)
test_indices = np.array(list(set(range(len(x_vals))) - set(train_ indices)))
x_vals_train = x_vals[train_indices]
x_vals_test = x_vals[test_indices]
y_vals_train = y_vals[train_indices]
y_vals_test = y_vals[test_indices]


4.Logistic regression convergence works better when the features are scaled between 0 and 1 (min-max scaling). So next we will scale each feature:
def normalize_cols(m):
col_max = m.max(axis=0)
col_min = m.min(axis=0)
return (m-col_min) / (col_max - col_min)
x_vals_train = np.nan_to_num(normalize_cols(x_vals_train))
x_vals_test = np.nan_to_num(normalize_cols(x_vals_test))
Note that we split the dataset into train and test before we scaled the dataset. This is an important distinction to make. We want to make sure that the training set does not influence the test set at all. If we scaled the whole set before splitting, then we cannot guarantee that they don't influence each other.

5.Now we can start our training loop and recording the loss and accuracies:
loss_vec = []
train_acc = []
test_acc = []
for i in range(1500):
rand_index = np.random.choice(len(x_vals_train), size=batch_ size)
rand_x = x_vals_train[rand_index]
rand_y = np.transpose([y_vals_train[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_ target: rand_y})
loss_vec.append(temp_loss)
temp_acc_train = sess.run(accuracy, feed_dict={x_data: x_vals_ train, y_target: np.transpose([y_vals_train])})
train_acc.append(temp_acc_train)
temp_acc_test = sess.run(accuracy, feed_dict={x_data: x_vals_ test, y_target: np.transpose([y_vals_test])})
test_acc.append(temp_acc_test)


6.Here is the code to look at the plots of the loss and accuracies:

plt.plot(loss_vec, 'k-')
plt.title('Cross Entropy Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('Cross' Entropy Loss')
plt.show()
plt.plot(train_acc, 'k-', label='Train Set Accuracy')
plt.plot(test_acc, 'r--', label='Test Set Accuracy')
plt.title('Train' and Test Accuracy')
plt.xlabel('Generation')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()

How it works…
Here is the loss over the iterations and train and test set accuracies. Since the dataset is only 189 observations, the train and test accuracy plots will change owing to the random splitting of the dataset:

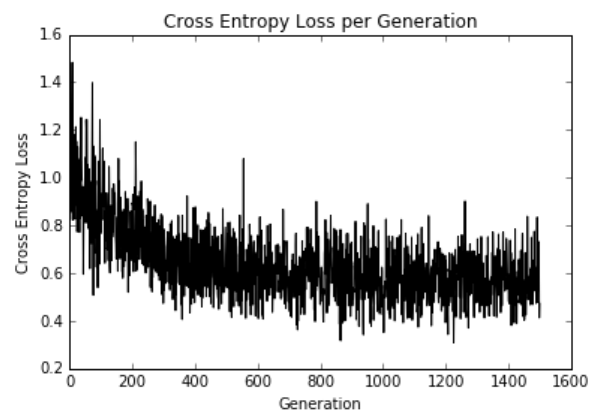
Figure 11: Cross-entropy loss plotted over the course of 1,500 iterations

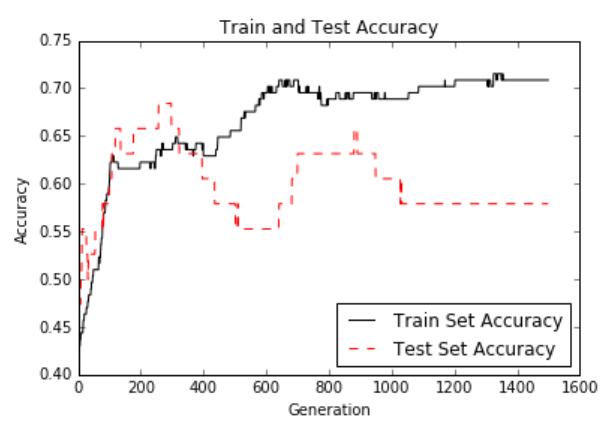
Figure 12: Test and train set accuracy plotted over 1,500 generations.

这帖子很不错