大数据技术之高频面试题(一)：面试说明与排序代码

问题导读：
1、面试过程最关键的是什么？
2、面试时该怎么说？
3、有哪些面试技巧？
4、如何手写排序代码？



第1章 面试说明

1.1 面试过程最关键的是什么？

1）不是你说了什么，而是你怎么说
2）大大方方的聊，放松

1.2 面试时该怎么说？
1）语言表达清楚
        （1）思维逻辑清晰，表达流畅
        （2）一二三层次表达

2）所述内容不犯错
        （1）不说前东家或者自己的坏话
        （2）往自己擅长的方面说
        （3）实质，对考官来说，内容听过，就是自我肯定；没听过，那就是个学习的过程。

1.3 面试技巧
1.3.1 六个常见问题

1）你的优点是什么？
        大胆的说出自己各个方面的优势和特长
2）你的缺点是什么？
        不要谈自己真实问题；用“缺点”衬托自己的优点

3）你的离职原因是什么？

• 不说前东家坏话，哪怕被伤过
• 合情合理合法
• 不要说超过1个以上的原因
  

4）您对薪资的期望是多少？

• 非终面不深谈薪资
• 只说区间，不说具体数字
• 底线是不低于当前薪资
• 非要具体数字，区间取中间值，或者当前薪资的+20%
  

5）您还有什么想问的问题？

• 这是体现个人眼界和层次的问题
• 问题本身不在于面试官想得到什么样的答案，而在于你跟别的应聘者的对比
• 标准答案：
  

公司希望我入职后的3-6个月内，给公司解决什么样的问题
公司（或者对这个部门）未来的战略规划是什么样子的？
以你现在对我的了解，您觉得我需要多长时间融入公司？

6）您最快多长时间能入职？
        一周左右，如果公司需要，可以适当提前

1.3.2 两个注意事项
1）职业化的语言
2）职业化的形象


1.3.3 自我介绍（控制在4分半以内，不超过5分钟）
1）个人基本信息
2）工作履历
        时间、公司名称、任职岗位、主要工作内容、工作业绩、离职原因

3）深度沟通（也叫压力面试）
        刨根问底下沉式追问（注意是下沉式，而不是发散式的）
        基本技巧：往自己熟悉的方向说


第2章 手写代码
2.1 冒泡排序

/**
* 冒泡排序 时间复杂度 O(n^2) 空间复杂度O(1)
*/
public class BubbleSort {
   public static void bubbleSort(int[] data) {
      System.out.println("开始排序");
      int arrayLength = data.length;
      for (int i = 0; i < arrayLength - 1; i++) {
         boolean flag = false;
         for (int j = 0; j < arrayLength - 1 - i; j++) {
            if(data[j] > data[j + 1]){
               int temp = data[j + 1];
               data[j + 1] = data[j];
               data[j] = temp;
               flag = true;
            }
         }
         System.out.println(java.util.Arrays.toString(data));
         if (!flag)
            break;
      }
   }
   public static void main(String[] args) {
      int[] data = { 9, -16, 21, 23, -30, -49, 21, 30, 30 };
      System.out.println("排序之前：\n" + java.util.Arrays.toString(data));
      bubbleSort(data);
      System.out.println("排序之后：\n" + java.util.Arrays.toString(data));
   }
}

2.2 二分查找

图4-二分查找核心思路

实现代码：
/**
 * 二分查找 时间复杂度O(log2n);空间复杂度O(1)
 */

def binarySearch(arr:Array[Int],left:Int,right:Int,findVal:Int): Int={
  if(left>right){//递归退出条件，找不到，返回-1
    -1
  }

  val midIndex = (left+right)/2

  if (findVal < arr(midIndex)){//向左递归查找
    binarySearch(arr,left,midIndex,findVal)
  }else if(findVal > arr(midIndex)){//向右递归查找
    binarySearch(arr,midIndex,right,findVal)
  }else{//查找到，返回下标
    midIndex
  }
}
复制代码

拓展需求：当一个有序数组中，有多个相同的数值时，如何将所有的数值都查找到。
代码实现如下：

/*
  {1,8, 10, 89, 1000, 1000，1234} 当一个有序数组中，有多个相同的数值时，如何将所有的数值都查找到，比如这里的 1000.
  //分析
  1. 返回的结果是一个可变数组 ArrayBuffer
  2. 在找到结果时，向左边扫描，向右边扫描 [条件]
  3. 找到结果后，就加入到ArrayBuffer
   */
  def binarySearch2(arr: Array[Int], l: Int, r: Int,
                    findVal: Int): ArrayBuffer[Int] = {

    //找不到条件?
    if (l > r) {
      return ArrayBuffer()
    }

    val midIndex = (l + r) / 2
    val midVal = arr(midIndex)
    if (midVal > findVal) {
      //向左进行递归查找
      binarySearch2(arr, l, midIndex - 1, findVal)
    } else if (midVal < findVal) { //向右进行递归查找
      binarySearch2(arr, midIndex + 1, r, findVal)
    } else {
      println("midIndex=" + midIndex)
      //定义一个可变数组
      val resArr = ArrayBuffer[Int]()
      //向左边扫描
      var temp = midIndex - 1
      breakable {
        while (true) {
          if (temp < 0 || arr(temp) != findVal) {
            break()
          }
          if (arr(temp) == findVal) {
            resArr.append(temp)
          }
          temp -= 1
        }
      }
      //将中间这个索引加入
      resArr.append(midIndex)
      //向右边扫描
      temp = midIndex + 1
      breakable {
        while (true) {
          if (temp > arr.length - 1 || arr(temp) != findVal) {
            break()
          }
          if (arr(temp) == findVal) {
            resArr.append(temp)
          }
          temp += 1
        }
      }
      return resArr
    }
复制代码

2.3 快排


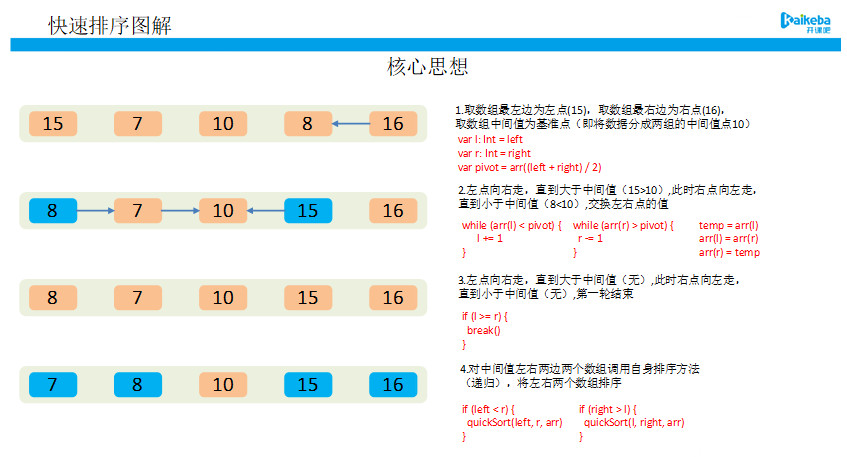
图1-快速排序核心思想

代码实现：
/**
 * 快排 
 * 时间复杂度:平均时间复杂度为O(nlogn)
 * 空间复杂度:O(logn)，因为递归栈空间的使用问题
 */
def quickSort(list: List[Int]): List[Int] = list match {
    case Nil => Nil
    case List() => List()
    case head :: tail =>
      val (left, right) = tail.partition(_ < head)
      quickSort(left) ::: head :: quickSort(right)
  }
复制代码

2.4 归并


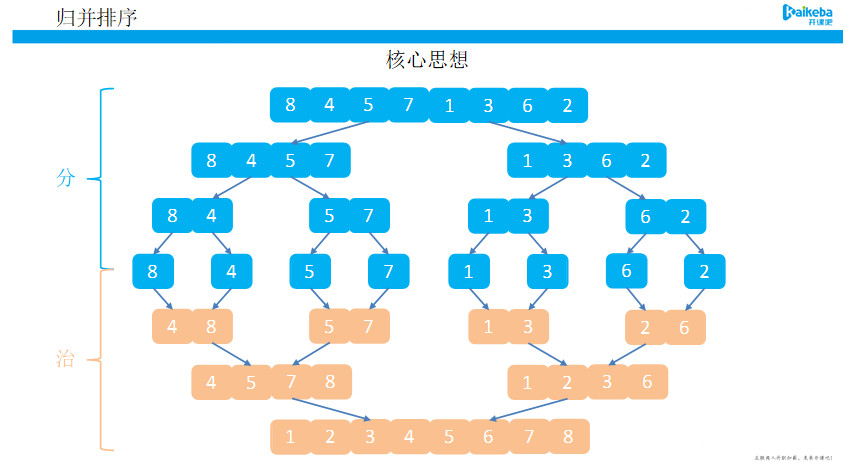
图2-归并排序核心思想
核心思想：不断的将大的数组分成两个小数组，直到不能拆分为止，即形成了单个值。此时使用合并的排序思想对已经有序的数组进行合并，合并为一个大的数据，不断重复此过程，直到最终所有数据合并到一个数组为止。

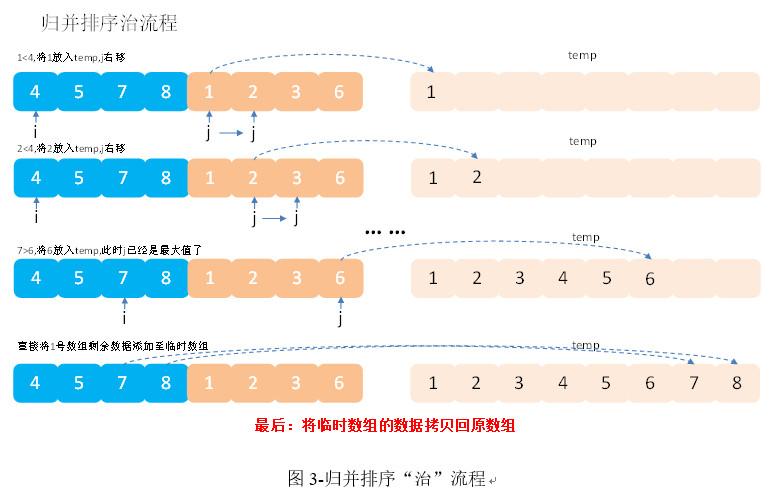
代码实现：
/**
 * 快排 
 * 时间复杂度:O(nlogn)
 * 空间复杂度:O(n)
 */
def merge(left: List[Int], right: List[Int]): List[Int] = (left, right) match {
    case (Nil, _) => right
    case (_, Nil) => left
    case (x :: xTail, y :: yTail) =>
      if (x <= y) x :: merge(xTail, right)
      else y :: merge(left, yTail)
  }
复制代码

2.5  二叉树之Scala实现
2.5.1 二叉树概念


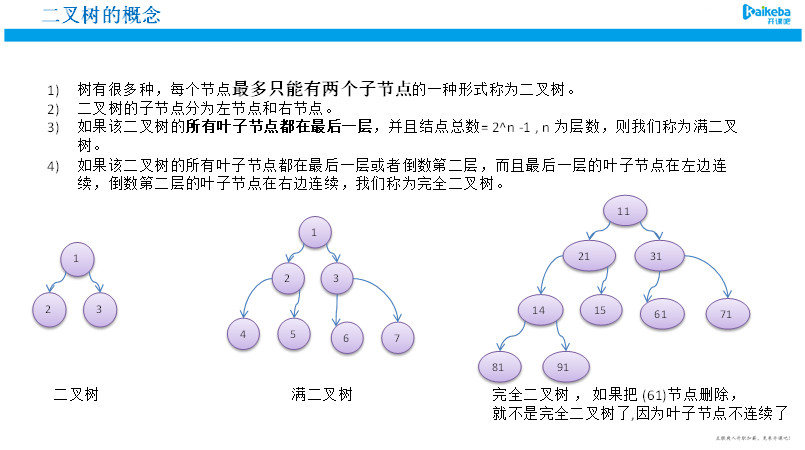
2.5.2 二叉树的特点
1）树执行查找、删除、插入的时间复杂度都是O(logN)
2）遍历二叉树的方法包括前序、中序、后序
3）非平衡树指的是根的左右两边的子节点的数量不一致
4） 在非空二叉树中，第i层的结点总数不超过 , i>=1；
5）深度为h的二叉树最多有个结点(h>=1)，最少有h个结点；
6）对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；

2.5.3 二叉树的Scala代码实现
定义节点以及前序、中序、后序遍历

class TreeNode(treeNo:Int){
  val no = treeNo
  var left:TreeNode = null
  var right:TreeNode = null

  //后序遍历
  def postOrder():Unit={
    //向左递归输出左子树
    if(this.left != null){
      this.left.postOrder
    }
    //向右递归输出右子树
    if (this.right != null) {
      this.right.postOrder
    }

    //输出当前节点值
    printf("节点信息 no=%d \n",no)
  }

  //中序遍历
  def infixOrder():Unit={
    //向左递归输出左子树
    if(this.left != null){
      this.left.infixOrder()
    }

    //输出当前节点值
    printf("节点信息 no=%d \n",no)

    //向右递归输出右子树
    if (this.right != null) {
      this.right.infixOrder()
    }
  }

  //前序遍历
  def preOrder():Unit={
    //输出当前节点值
    printf("节点信息 no=%d \n",no)

    //向左递归输出左子树
    if(this.left != null){
      this.left.postOrder()
    }

    //向右递归输出右子树
    if (this.right != null) {
      this.right.preOrder()
    }
  }

  //后序遍历查找
  def postOrderSearch(no:Int): TreeNode = {
    //向左递归输出左子树
    var resNode:TreeNode = null
    if (this.left != null) {
      resNode = this.left.postOrderSearch(no)
    }
    if (resNode != null) {
      return resNode
    }
    if (this.right != null) {
      resNode = this.right.postOrderSearch(no)
    }
    if (resNode != null) {
      return resNode
    }
    println("ttt~~")
    if (this.no == no) {
      return this
    }
    resNode
  }

  //中序遍历查找
  def infixOrderSearch(no:Int): TreeNode = {


    var resNode : TreeNode = null
    //先向左递归查找
    if (this.left != null) {
      resNode = this.left.infixOrderSearch(no)
    }
    if (resNode != null) {
      return resNode
    }
    println("yyy~~")
    if (no == this.no) {
      return this
    }
    //向右递归查找
    if (this.right != null) {
      resNode = this.right.infixOrderSearch(no)
    }
    return resNode

  }

  //前序查找
  def preOrderSearch(no:Int): TreeNode = {
    if (no == this.no) {
      return this
    }
    //向左递归查找
    var resNode : TreeNode = null
    if (this.left != null) {
      resNode = this.left.preOrderSearch(no)
    }
    if (resNode != null){
      return  resNode
    }
    //向右边递归查找
    if (this.right != null) {
      resNode = this.right.preOrderSearch(no)
    }

    return resNode
  }

  //删除节点
  //删除节点规则
  //1如果删除的节点是叶子节点，则删除该节点
  //2如果删除的节点是非叶子节点，则删除该子树

  def delNode(no:Int): Unit = {
    //首先比较当前节点的左子节点是否为要删除的节点
    if (this.left != null && this.left.no == no) {
      this.left = null
      return
    }
    //比较当前节点的右子节点是否为要删除的节点
    if (this.right != null && this.right.no == no) {
      this.right = null
      return
    }
    //向左递归删除
    if (this.left != null) {
      this.left.delNode(no)
    }
    //向右递归删除
    if (this.right != null) {
      this.right.delNode(no)
    }
  }
}
复制代码

定义二叉树，前序、中序、后序遍历，前序、中序、后序查找，删除节点

class BinaryTree{
  var root:TreeNode = null

  //后序遍历
  def postOrder(): Unit = {
    if (root != null){
      root.postOrder()
    }else {
      println("当前二叉树为空，不能遍历")
}
}
    //中序遍历
    def infixOrder(): Unit = {
      if (root != null){
        root.infixOrder()
      }else {
        println("当前二叉树为空，不能遍历")
      }
    }
    //前序遍历
    def preOrder(): Unit = {
      if (root != null){
        root.preOrder()
      }else {
        println("当前二叉树为空，不能遍历")
      }
    }

    //后序遍历查找
    def postOrderSearch(no:Int): TreeNode = {
      if (root != null) {
        root.postOrderSearch(no)
      }else{
        null
      }
    }

    //中序遍历查找
    def infixOrderSeacher(no:Int): TreeNode = {
      if (root != null) {
        return root.infixOrderSearch(no)
      }else {
        return null
      }
    }

    //前序查找
    def preOrderSearch(no:Int): TreeNode = {

      if (root != null) {
        return root.preOrderSearch(no)
      }else{
        //println("当前二叉树为空，不能查找")
        return null
      }
    }
//删除节点
    def delNode(no:Int): Unit = {
      if (root != null) {
        //先处理一下root是不是要删除的
        if (root.no == no){
          root = null
        }else {
          root.delNode(no)
        }
      }
    
  }
复制代码

2.6 手写Spark-WordCount

val conf: SparkConf = 
new SparkConf().setMaster("local[*]").setAppName("WordCount")

val sc = new SparkContext(conf)

sc.textFile("/input")
  .flatMap(_.split(" "))
  .map((_, 1))
  .reduceByKey(_ + _)
  .saveAsTextFile("/output")

sc.stop()

复制代码

2.7 手写Spark程序
要求：(a,1) (a,3) (b,3) (b,5) (c,4)，求每个key对应value的平均值

rdd.combineByKey(v=>(v,1),(acc:(Int,Int),newV)=>(acc._1+newV,acc._2+1),(acc1:(Int,Int),acc2:(Int,Int))=>(acc1._1+acc2._1,acc1._2+acc2._2))
复制代码

最新经典文章，欢迎关注公众号