TensorFlow ML cookbook 第四章1节 应用线性SVM

问题导读：
1、如何理解支持向量机？
2、如何理解软边际损失函数？
3、如何声明L2范数函数？
4、如何应用SVM算法？




上一篇:TensorFlow ML cookbook 第三章6-8节 套索和岭回归、弹性网络回归and Logistic回归

支持向量机

本章将介绍有关如何在TensorFlow中使用、实现和评估支持向量机（SVM）的一些重要方法。 将涵盖以下领域：

• 使用线性SVM
• 减少到线性回归
• 在TensorFlow中使用内核
• 实现非线性SVM
• 实现多类SVM
  

请注意，本章中先前涵盖的逻辑回归和大多数SVM都是二元预测变量。 虽然逻辑回归试图找到最大化距离的任何分离线（概率地），但SVM还试图最小化误差，同时最大化类之间的余量。 通常，如果问题与训练示例相比具有大量特征，请尝试逻辑回归或线性SVM。 如果训练样本的数量较大，或者数据不是线性可分的，则可以使用具有高斯核的SVM。
还要记住，本章的所有代码都可以在线获取https://github. com/nfmcclure/tensorflow_cookbook.

介绍
支持向量机是一种二元分类方法。 基本思想是在两个类之间找到线性分离线（或超平面）。 我们首先假设二进制类目标是-1或1，而不是先前的0或1目标。 由于可能有许多行分隔两个类，因此我们定义了最大化线性分隔符，以最大化两个类之间的距离。

图1：给定两个可分类，'o'和'x'，我们希望找到两者之间的线性分离器的等式。 左侧显示有许多行将两个类分开。 右侧显示唯一的最大边距线。 边距宽度为2 /||A||。 通过最小化A的L2范数找到该线。
我们可以编写如下超平面：Ax-b = 0
这里，A是我们的部分斜率的向量，x是输入的向量。 最大边距的宽度可以显示为2除以A的L2范数。这个事实有很多证明，但对于几何思想，求解从2D点到直线的垂直距离可以提供动力 向前迈进 对于线性可分的二进制类数据，为了最大化余量，我们最小化A的L2范数，||A||我们还必须将这个最小值置于约束之下：

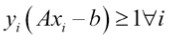
前面的约束确保我们来自相应类的所有点都在分离线的同一侧。
由于并非所有数据集都是线性可分的，因此我们可以为跨越边界线的点引入损失函数。 对于n个数据点，我们引入了所谓的软边际损失函数，如下所示：

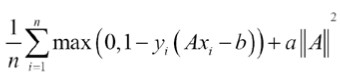
注意该产品 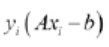如果该点位于边距的正确边上，则始终大于1。 这使得损失函数的左项等于零，并且对损失函数的唯一影响是边际的大小。
前面的损失函数将寻找线性可分的线，但允许穿过边缘线的点。 这可以是硬性或软性允许值，具体取决于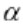值 更大的价值 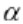导致更加强调扩大利润率和更小的价值 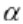导致模型更像是一个硬边缘，同时允许数据点越过边距，如果需要的话。

在本章中，我们将设置一个软边界SVM，并展示如何将其扩展到非线性情况和多个类。
使用线性SVM
对于此示例，我们将从虹膜数据集创建线性分隔符。 我们从前面的章节中知道，萼片长度和花瓣宽度创建了一个线性可分的二进制数据集，用于预测花是否是I. setosa。

做好准备
要在TensorFlow中实现软可分SVM，我们将实现特定的损失函数，如下所示：


怎么做
1.我们首先加载必要的库。 这将包括用于访问虹膜数据集的scikit learn数据集库。 使用以下代码：
[mw_shl_code=python,true]import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets[/mw_shl_code]
要设置Scikit-learn进行此练习，我们只需要键入$ pip install -U scikit-learn。 请注意，它也安装了Anaconda。

2.接下来我们开始图形会话并根据需要加载数据。 请记住，我们正在加载虹膜数据集中的第一个和第四个变量，因为它们是萼片长度和萼片宽度。 我们正在加载目标变量，对于I. setosa将取值1，否则为-1。 使用以下代码：
[mw_shl_code=python,true]sess = tf.Session()
iris = datasets.load_iris()
x_vals = np.array([[x[0], x[3]] for x in iris.data])
y_vals = np.array([1 if y==0 else -1 for y in iris.target])
[/mw_shl_code]
3.我们现在应该将数据集拆分为训练集和测试集。 我们将评估训练和测试集的准确性。 由于我们知道这个数据集是线性可分的，因此我们应该期望在两个集合上获得百分之百的准确度。 使用以下代码：
[mw_shl_code=python,true]train_indices = np.random.choice(len(x_vals), round(len(x_ vals)*0.8), replace=False)
test_indices = np.array(list(set(range(len(x_vals))) - set(train_ indices)))
x_vals_train = x_vals[train_indices]
x_vals_test = x_vals[test_indices]
y_vals_train = y_vals[train_indices]
y_vals_test = y_vals[test_indices][/mw_shl_code]

4.接下来我们设置批量大小，占位符和模型变量。 值得一提的是，使用这种SVM算法，我们需要非常大的批量大小来帮助收敛。 我们可以想象，对于非常小的批量大小，最大边际线会略微跳跃。 理想情况下，我们也会慢慢降低学习率，但现在这已经足够了。 此外，A变量将采用2x1的形状，因为我们有两个预测变量，即萼片长度和踏板宽度。 使用以下代码：
[mw_shl_code=python,true]batch_size = 100
x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
A = tf.Variable(tf.random_normal(shape=[2,1]))
b = tf.Variable(tf.random_normal(shape=[1,1])) [/mw_shl_code]

5.我们现在声明我们的模型输出。 对于正确分类的点，如果目标是I. setosa，则返回大于或等于1的数字，否则返回小于或等于-1。 使用以下代码：
[mw_shl_code=python,true]model_output = tf.sub(tf.matmul(x_data, A), b) [/mw_shl_code]

6.接下来我们将汇总并声明最大保证金损失的必要组成部分。 首先，我们将声明一个计算向量的L2范数的函数。 然后我们添加margin参数。 然后我们宣布我们的分类损失并将这两个术语加在一起。 使用以下代码：
[mw_shl_code=python,true]l2_norm = tf.reduce_sum(tf.square(A))
alpha = tf.constant([0.1])
classification_term = tf.reduce_mean(tf.maximum(0., tf.sub(1., tf.mul(model_output, y_target))))
loss = tf.add(classification _term, tf.mul(alpha, l2_norm)) [/mw_shl_code]

7.现在我们宣布我们的预测和准确度函数，以便我们可以评估训练和测试集的准确性，如下所示;
[mw_shl_code=python,true]prediction = tf.sign(model_output)
accuracy = tf.reduce_mean(tf.cast(tf.equal(prediction, y_target), tf.float32))[/mw_shl_code]

8.这里我们将声明我们的优化器函数并初始化我们的模型变量，如下所示：
[mw_shl_code=python,true]my_opt = tf.train.GradientDescentOptimizer(0.01)
train_step = my_opt.minimize(loss)
init = tf.initialize_all_variables()
sess.run(init) [/mw_shl_code]

9.我们现在可以开始我们的训练循环，记住我们想要在训练和测试集上记录我们的损失和训练准确性，如下所示：
[mw_shl_code=python,true]loss_vec = []
train_accuracy = []
test_accuracy = []
for i in range(500):
rand_index = np.random.choice(len(x_vals_train), size=batch_ size)
rand_x = x_vals_train[rand_index]
rand_y = np.transpose([y_vals_train[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_ target: rand_y})
loss_vec.append(temp_loss)
train_acc_temp = sess.run(accuracy, feed_dict={x_data: x_vals_ train, y_target: np.transpose([y_vals_train])})
train_accuracy.append(train_acc_temp)
test_acc_temp = sess.run(accuracy, feed_dict={x_data: x_vals_ test, y_target: np.transpose([y_vals_test])})
test_accuracy.append(test_acc_temp)
if (i+1)%100==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
print('Loss = ' + str(temp_loss))

10.训练期间脚本的输出应如下所示。
Step #100 A = [[-0.10763293]
[-0.65735245]] b = [[-0.68752676]]
Loss = [ 0.48756418]
Step #200 A = [[-0.0650763 ]
[-0.89443302]] b = [[-0.73912662]]
Loss = [ 0.38910741]
Step #300 A = [[-0.02090022]
[-1.12334013]] b = [[-0.79332656]]
Loss = [ 0.28621092]
Step #400 A = [[ 0.03189624]
[-1.34912157]] b = [[-0.8507266]]
Loss = [ 0.22397576]
Step #500 A = [[ 0.05958777]
[-1.55989814]] b = [[-0.9000265]]
Loss = [ 0.20492229] [/mw_shl_code]

11.为了绘制输出，我们必须提取系数并将x值分成I. setosa和非I. setosa，如下所示：
[mw_shl_code=python,true][[a1], [a2]] = sess.run(A)
[] = sess.run(b)
slope = -a2/a1
y_intercept = b/a1
x1_vals = [d[1] for d in x_vals]
best_fit = []
for i in x1_vals:
best_fit.append(slope*i+y_intercept)
setosa_x = [d[1] for i,d in enumerate(x_vals) if y_vals==1]
setosa_y = [d[0] for i,d in enumerate(x_vals) if y_vals==1]
not_setosa_x = [d[1] for i,d in enumerate(x_vals) if y_ vals==-1]
not_setosa_y = [d[0] for i,d in enumerate(x_vals) if y_ vals==-1] [/mw_shl_code]

12.以下是使用线性分隔符，精度和损耗绘制数据的代码：
[mw_shl_code=python,true]plt.plot(setosa_x, setosa_y, 'o', label='I. setosa')
plt.plot(not_setosa_x, not_setosa_y, 'x', label='Non-setosa')
plt.plot(x1_vals, best_fit, 'r-', label='Linear Separator', linewidth=3)
plt.ylim([0, 10])
plt.legend(loc='lower right')
plt.title('Sepal Length vs Pedal Width')
plt.xlabel('Pedal Width')
plt.ylabel('Sepal Length')
plt.show()
plt.plot(train_accuracy, 'k-', label='Training Accuracy')
plt.plot(test_accuracy, 'r--', label='Test Accuracy')
plt.title('Train and Test Set Accuracies')
plt.xlabel('Generation')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()
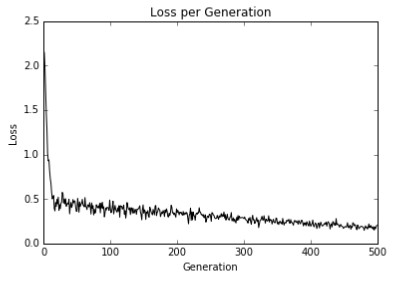
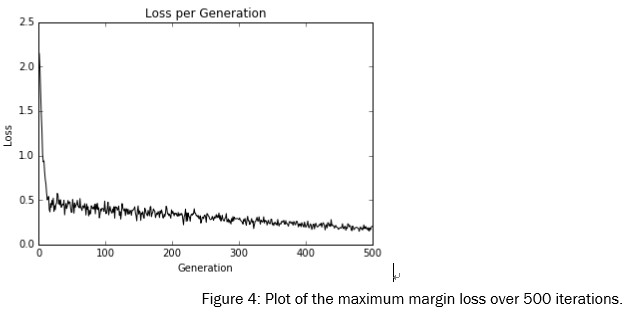
plt.plot(loss_vec, 'k-')
plt.title('Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()[/mw_shl_code]
以这种方式使用TensorFlow来实现SVD算法可能导致每次运行的结果略有不同。 其原因包括随机训练/测试集拆分以及每个训练批次中不同批次点的选择。 同样，在每一代之后慢慢降低学习率也是理想的。

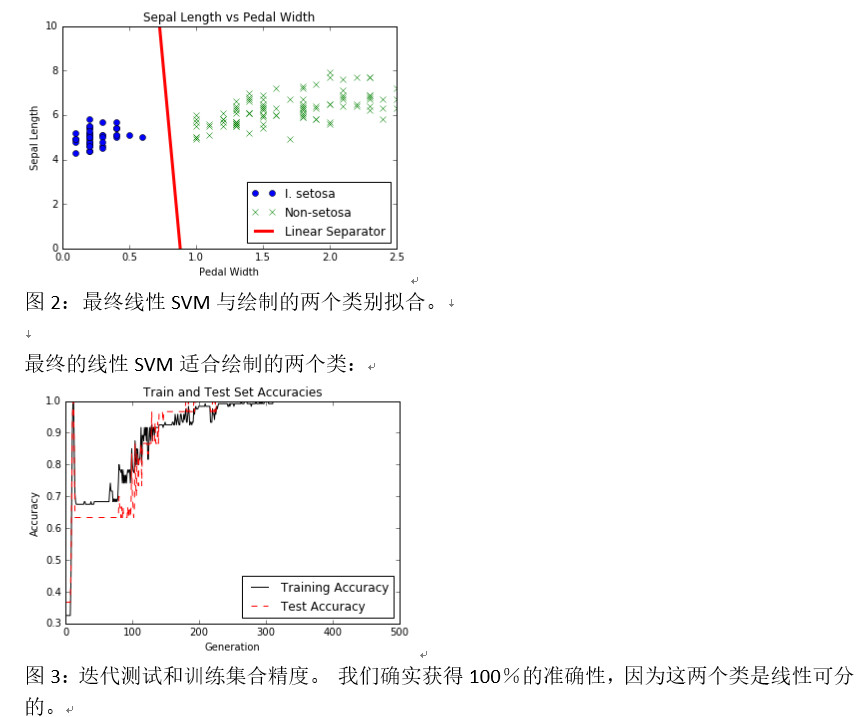
在迭代中测试和训练设定精度。 我们确实获得100％的准确性，因为这两个类是线性可分的：


怎么运行
在本文中，我们已经证明通过使用最大边际损失函数可以实现线性SVD模型。



原文：
Support Vector Machines

This chapter will cover some important recipes regarding how to use, implement, and evaluate support vector machines (SVM) in TensorFlow. The following areas will be covered:

• Working with a Linear SVM
• Reduction to Linear Regression
• Working with Kernels in TensorFlow
• Implementing a Non-Linear SVM
• Implementing a Multi-Class SVM
  

Note that both the prior covered logistic regression and most of the SVMs in this chapter are binary predictors. While logistic regression tries to find any separating line that maximizes the distance (probabilistically), SVMs also try to minimize the error while maximizing the margin between classes. In general, if the problem has a large number of features compared to training examples, try logistic regression or a linear SVM. If the number of training examples is larger, or the data is not linearly separable, a SVM with a Gaussian kernel may be used.
Also remember that all the code for this chapter is available online at https://github. com/nfmcclure/tensorflow_cookbook.
Introduction
Support vector machines are a method of binary classification. The basic idea is to find a linear separating line (or hyperplane) between the two classes. We first assume that the binary class targets are -1 or 1, instead of the prior 0 or 1 targets. Since there may be many lines that separate two classes, we define the best linear separator that maximizes the distance between both classes.


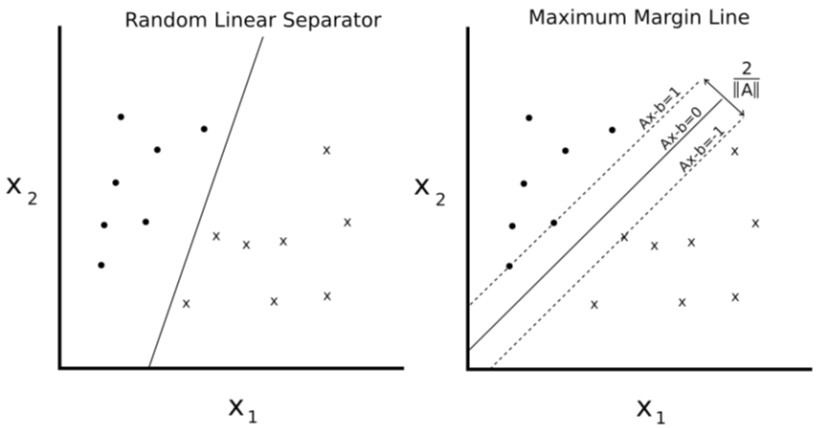
Figure 1: Given two separable classes, 'o' and 'x', we wish to find the equation for the linear separator between the two. The left shows that there are many lines that separate the two classes. The right shows the unique maximum margin line. The margin width is given by 2/||A||. This line is found by minimizing the L2 norm of A.
We can write such a hyperplane as follows:
Ax-b=0
Here, A is a vector of our partial slopes and x is a vector of inputs. The width of the maximum margin can be shown to be two divided by the L2 norm of A. There are many proofs out there of this fact, but for a geometric idea, solving the perpendicular distance from a 2D point to a line may provide motivation for moving forward.
For linearly separable binary class data, to maximize the margin, we minimize the L2 norm of A, ||A||We must also subject this minimum to the constraint:


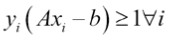
The preceding constraint assures us that all the points from the corresponding classes are on the same side of the separating line.
Since not all datasets are linearly separable, we can introduce a loss function for points that cross the margin lines. For n data points, we introduce what is called the soft margin loss function, as follows:


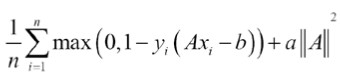
Note that the product 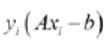s always greater than 1 if the point is on the correct side of the margin. This makes the left term of the loss function equal to zero, and the only influence on the loss function is the size of the margin.
The preceding loss function will seek a linearly separable line, but will allow for points crossing the margin line. This can be a hard or soft allowance, depending on the value of. Larger values of 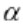result in more emphasis on widening the margin, and smaller values ofresult in the model acting more like a hard margin, while allowing data points to cross the margin, if need be.
In this chapter, we will set up a soft margin SVM and show how to extend it to nonlinear cases and multiple classes.


Working with a Linear SVM
For this example, we will create a linear separator from the iris data set. We know from prior chapters that the sepal length and petal width create a linear separable binary data set for predicting if a flower is I. setosa or not.


Getting ready
To implement a soft separable SVM in TensorFlow, we will implement the specific loss function, as follows:

How to do it…
1.We start by loading the necessary libraries. This will include the scikit learn dataset library for access to the iris data set. Use the following code:
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from sklearn import datasets
To set up Scikit-learn for this exercise, we just need to type $pip install –U scikit-learn. Note that it also comes installed with Anaconda as well.


2.Next we start a graph session and load the data as we need it. Remember that we are loading the first and fourth variables in the iris dataset as they are the sepal length and sepal width. We are loading the target variable, which will take on the value 1 for I. setosa and -1 otherwise. Use the following code:
sess = tf.Session()
iris = datasets.load_iris()
x_vals = np.array([[x[0], x[3]] for x in iris.data])
y_vals = np.array([1 if y==0 else -1 for y in iris.target])
3.We should now split the dataset into train and test sets. We will evaluate the accuracy on both the training and test sets. Since we know this data set is linearly separable, we should expect to get one hundred percent accuracy on both sets. Use the following code:

train_indices = np.random.choice(len(x_vals), round(len(x_ vals)*0.8), replace=False)
test_indices = np.array(list(set(range(len(x_vals))) - set(train_ indices)))
x_vals_train = x_vals[train_indices]
x_vals_test = x_vals[test_indices]
y_vals_train = y_vals[train_indices]
y_vals_test = y_vals[test_indices]


4.Next we set our batch size, placeholders, and model variables. It is important to mention that with this SVM algorithm, we want very large batch sizes to help with convergence. We can imagine that with very small batch sizes, the maximum margin line would jump around slightly. Ideally, we would also slowly decrease the learning rate as well, but this will suffice for now. Also, the A variable will take on the shape 2x1 because we have two predictor variables, sepal length and pedal width. Use the following code:
batch_size = 100
x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
A = tf.Variable(tf.random_normal(shape=[2,1]))
b = tf.Variable(tf.random_normal(shape=[1,1]))
5.We now declare our model output. For correctly classified points, this will return numbers that are greater than or equal to 1 if the target is I. setosa and less than or equal to -1 otherwise. Use the following code:

model_output = tf.sub(tf.matmul(x_data, A), b)
6.Next we will put together and declare the necessary components for the maximum margin loss. First we will declare a function that will calculate the L2 norm of a vector. Then we add the margin parameter, . We then declare our classification loss and add together the two terms. Use the following code:

l2_norm = tf.reduce_sum(tf.square(A))
alpha = tf.constant([0.1])
classification_term = tf.reduce_mean(tf.maximum(0., tf.sub(1., tf.mul(model_output, y_target))))
loss = tf.add(classification _term, tf.mul(alpha, l2_norm))
7.Now we declare our prediction and accuracy functions so that we can evaluate the accuracy on both the training and test sets, as follows;
prediction = tf.sign(model_output)
accuracy = tf.reduce_mean(tf.cast(tf.equal(prediction, y_target), tf.float32))



8.Here we will declare our optimizer function and initialize our model variables, as follows:
my_opt = tf.train.GradientDescentOptimizer(0.01)
train_step = my_opt.minimize(loss)
init = tf.initialize_all_variables()
sess.run(init)
9.We now can start our training loop, keeping in mind that we want to record our loss and training accuracy on both the training and test set, as follows:
loss_vec = []
train_accuracy = []
test_accuracy = []
for i in range(500):
rand_index = np.random.choice(len(x_vals_train), size=batch_ size)
rand_x = x_vals_train[rand_index]
rand_y = np.transpose([y_vals_train[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_ target: rand_y})
loss_vec.append(temp_loss)
train_acc_temp = sess.run(accuracy, feed_dict={x_data: x_vals_ train, y_target: np.transpose([y_vals_train])})
train_accuracy.append(train_acc_temp)
test_acc_temp = sess.run(accuracy, feed_dict={x_data: x_vals_ test, y_target: np.transpose([y_vals_test])})
test_accuracy.append(test_acc_temp)
if (i+1)%100==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)) + ' b = ' + str(sess.run(b)))
print('Loss = ' + str(temp_loss))
10.The output of the script during training should look like the following.

Step #100 A = [[-0.10763293]
[-0.65735245]] b = [[-0.68752676]]
Loss = [ 0.48756418]
Step #200 A = [[-0.0650763 ]
[-0.89443302]] b = [[-0.73912662]]
Loss = [ 0.38910741]
Step #300 A = [[-0.02090022]
[-1.12334013]] b = [[-0.79332656]]
Loss = [ 0.28621092]
Step #400 A = [[ 0.03189624]
[-1.34912157]] b = [[-0.8507266]]
Loss = [ 0.22397576]
Step #500 A = [[ 0.05958777]
[-1.55989814]] b = [[-0.9000265]]
Loss = [ 0.20492229]
11.In order to plot the outputs, we have to extract the coefficients and separate the x values into I. setosa and non- I. setosa, as follows:

[[a1], [a2]] = sess.run(A)
[] = sess.run(b)
slope = -a2/a1
y_intercept = b/a1
x1_vals = [d[1] for d in x_vals]
best_fit = []
for i in x1_vals:
best_fit.append(slope*i+y_intercept)
setosa_x = [d[1] for i,d in enumerate(x_vals) if y_vals==1]
setosa_y = [d[0] for i,d in enumerate(x_vals) if y_vals==1]
not_setosa_x = [d[1] for i,d in enumerate(x_vals) if y_ vals==-1]
not_setosa_y = [d[0] for i,d in enumerate(x_vals) if y_ vals==-1]
12.The following is the code to plot the data with the linear separator, accuracies, and loss:
plt.plot(setosa_x, setosa_y, 'o', label='I. setosa')
plt.plot(not_setosa_x, not_setosa_y, 'x', label='Non-setosa')
plt.plot(x1_vals, best_fit, 'r-', label='Linear Separator', linewidth=3)
plt.ylim([0, 10])
plt.legend(loc='lower right')
plt.title('Sepal Length vs Pedal Width')
plt.xlabel('Pedal Width')
plt.ylabel('Sepal Length')
plt.show()
plt.plot(train_accuracy, 'k-', label='Training Accuracy')
plt.plot(test_accuracy, 'r--', label='Test Accuracy')
plt.title('Train and Test Set Accuracies')
plt.xlabel('Generation')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()
plt.plot(loss_vec, 'k-')
plt.title('Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()

Using TensorFlow in this manner to implement the SVD algorithm may result in slightly different outcomes each run. The reasons for this include the random train/test set splitting and the selection of different batches of points on each training batch. Also it would be ideal to also slowly lower the learning rate after each generation.


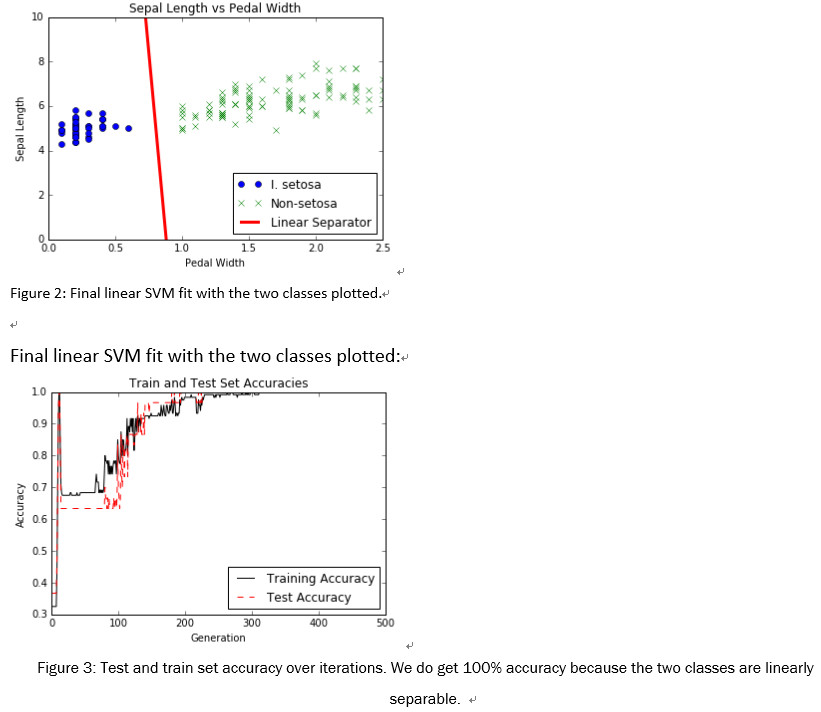
Test and train set accuracy over iterations. We do get 100% accuracy because the two classes are linearly separable:

How it works…
In this recipe, we have shown that implementing a linear SVD model is possible by using the maximum margin loss function.

感谢分享